




Key Takeaways
- ACT Math success requires both strategy and stamina, not just math skills.
- Smart time management prevents careless mistakes and boosts accuracy under pressure.
- Targeted practice builds confidence, efficiency, and scholarship-winning score gains.
The ACT Math section presents a formidable challenge that extends beyond mathematical knowledge alone. Even students with strong foundational skills can struggle with the section's demanding pace and strategic requirements. With 60 questions to solve in just 60 minutes (now 45 questions in 50 minutes on the new digital format), it demands not only math knowledge but also strategy and stamina.
This timing evolution actually represents an improvement: students gain about 6 more seconds per question on ACT Math with the new format. However, the pressure remains intense, as questions progress from basic algebra and geometry concepts to advanced trigonometry and coordinate geometry, requiring tutors to teach adaptive time management strategies.
As an ACT tutor, your mission extends far beyond reviewing math concepts. You're developing test-taking athletes who can maintain accuracy under pressure while navigating questions that deliberately include trap answers and time-consuming calculations.
In this guide, we’ll explore actionable tips—covering everything from time management to content mastery—that tutors can use to help students significantly improve their ACT Math performance.
Each tip is presented with a solution-focused approach as if guiding a student, ensuring you can directly apply these strategies in your tutoring sessions.
Why ACT Math deserves smart prep
The ACT Math score carries substantial weight in college admissions and scholarship decisions. A single test point can give you access to thousands of dollars in financial aid to pay for college, making strategic preparation a high-return investment.
Many universities offer automatic scholarships based purely on ACT scores: minimum test score requirements range from 27-34 on the ACT for guaranteed scholarships ranging from $1,000 up to the full federally approved cost of attendance.
For tutors, this financial reality transforms your role from academic support to financial advocate. A student who improves from a 26 to a 28 on the ACT doesn't just gain 2 points—they unlock guaranteed scholarship opportunities that may not have been available at the lower score threshold.
However, test anxiety can sabotage even well-prepared students on test day. Early, structured practice builds the confidence students need to perform under pressure, turning mathematical knowledge into actual points.
The most common student struggles
Time pressure chaos: With just over one minute per question on the enhanced ACT Math section (45 questions in 50 minutes), students frequently rush through problems, leading to a cascade of preventable errors. Time pressure is one of the primary causes of careless mistakes on standardized tests.
Formula amnesia: Under stress, even familiar formulas become difficult to recall. Students who confidently use mathematical formulas during practice may struggle to remember them during the actual test when anxiety and time pressure interfere with memory retrieval.
Word problem misinterpretation: Complex mathematical language combined with time pressure creates a perfect storm for misreading. Students often solve the wrong question entirely—calculating area when the problem asks for perimeter, or finding the slope when they need the y-intercept.
Strategic blindness: Many students approach every question the same way, missing opportunities to save time through estimation, elimination, or pattern recognition. They'll calculate 847 × 0.23 by hand instead of recognizing that only one answer choice is close to 200.
Why smart prep delivers results
Targeted intervention saves time: Generic math review wastes precious tutoring hours. Analytics-driven preparation identifies specific weaknesses—whether it's rational expressions, trigonometric identities, or coordinate transformations—allowing you to focus exclusively on high-impact areas.
Strategic techniques reduce cognitive load: Teaching students systematic approaches (like the 4-step Math Method: state the question, examine given information, choose an approach, confirm the answer) creates mental shortcuts that preserve working memory for complex calculations.
Confidence builds momentum: Each correctly solved practice problem reinforces neural pathways and builds test-taking confidence. Students who complete 500+ strategically chosen practice problems show measurably less test anxiety and maintain accuracy even under time pressure.
Data-driven optimization: Modern analytics platforms reveal exactly which question types, mathematical concepts, and timing strategies work best for each individual student. This precision eliminates guesswork and ensures every tutoring minute directly contributes to score improvement.
For ACT tutors, smart preparation isn't just about covering content—it's about building test-taking athletes who can execute under pressure while maximizing their scholarship potential.
Understand the ACT Math structure
Mastering the ACT Math section requires understanding both its format and content distribution. This knowledge allows tutors to create targeted preparation strategies and helps students allocate their study time effectively.
Format and timing
Current ACT Math format:
- Paper-based ACT: 60 questions in 60 minutes (exactly 1 minute per question)
- Digital ACT: 45 questions in 50 minutes (approximately 1 minute 7 seconds per question)
The digital format provides students with slightly more time per question, but the pressure remains intense. Pacing and problem solving are the big challenges on the ACT math section, requiring students to work both quickly and strategically.
Content distribution by topic
Understanding the weight of each mathematical area helps prioritize preparation time.
Primary content areas
- Pre-Algebra: 14 questions based on math terminology (integers, prime numbers), basic number theory (rules of zero, order of operations), and manipulation of fractions and decimals
- Elementary Algebra: 10 questions based on inequalities, linear equations, ratios, percentages, and averages
- Intermediate Algebra: 9 questions based on exponents, roots, simultaneous equations, and quadratic equations
- Plane Geometry: 14 questions based on angles, lengths, triangles, quadrilaterals, circles, perimeter, area, and volume
- Coordinate Geometry: 9 questions based on slope, distance, midpoint, parallel and perpendicular lines, points of intersection, and graphing
- Trigonometry: 4 questions on basic trigonometric functions and applications
Percentage breakdown
Approximately half of the problems cover Algebra and approximately 40% cover geometry. The remaining 10% covers concepts from middle school and some problems over high school Pre-calculus.
Question difficulty progression
The ACT questions progress in order of difficulty, starting with the easiest and ending with the hardest. This creates a strategic opportunity: students can build confidence and momentum with early questions while saving time for the more challenging problems that appear later.
Formula requirements
There is no overall formula sheet provided for the ACT. Some individual questions may provide a formula, but the majority won't. This stands in stark contrast to the SAT, which provides a reference sheet.
There's no way around it; a student's test-prep process must include memorizing formulas. Students must commit essential formulas to memory, including:
- Area and volume formulas for geometric figures
- Distance and midpoint formulas
- Quadratic formula
- Basic trigonometric ratios (SOH-CAH-TOA)
- Linear equation forms
Answer choices and guessing strategy
- Paper ACT: 5 answer choices (A, B, C, D, E)
- Digital ACT: 4 answer choices—great news for students guessing on questions, since it will increase chances of getting questions right from 20% to 25%
No penalty for guessing: Every question is multiple choice, and there is no penalty for guessing. This means students should answer every question, even if they must guess.
Digital vs. paper format differences
The enhanced digital ACT brings several changes beyond timing:
- Students gain about 6 more seconds per question on ACT Math
- Built-in calculator available (though approved handheld calculators still permitted)
- The ACT has said that it plans to eliminate what was the most obviously incorrect answer from the answer options
The new ACT changes that split to 80% high-school concepts and 20% pre-high-school concepts, meaning more advanced mathematical reasoning will be required.
For tutors, this structural knowledge allows you to create realistic practice conditions, teach strategic time management, and ensure students are prepared for the specific demands of their chosen test format.
Time management strategies tutors should teach
Time management represents the defining factor between students who know the math and students who score well on the ACT Math section. The brutal arithmetic is unforgiving: 60 questions in 60 minutes (exactly 1 minute per question) for paper ACT, or 45 questions in 50 minutes (approximately 1 minute 7 seconds per question) for digital format.
Yet, this average masks a critical reality—questions vary dramatically in complexity, and successful students must develop sophisticated pacing strategies that go far beyond simply "working faster."
Students frequently report knowing how to solve problems they never attempted, highlighting that time management failures directly translate to point losses. The psychological pressure compounds this challenge, as students who fall behind schedule often make careless errors on problems they could easily solve under normal conditions. Effective tutoring must transform time management from a source of anxiety into a strategic advantage.
Strategy 1: Master the strategic skip-and-return system
The most powerful time management technique involves recognizing when to abandon a problem temporarily rather than getting trapped in time-consuming struggles. This strategy prevents the cascade failure where one difficult problem destroys timing for the entire section.
The 30-second decision rule: If a student hasn't identified a clear solution path within 30 seconds, they should flag the question and move on. This threshold prevents students from spending 3-4 minutes on a single problem while easier questions remain unattempted.
Systematic flagging protocol:
- Circle the question number: Create a quick visual marker for return visits.
- Eliminate obvious wrong answers: Before moving on, cross out clearly incorrect choices to improve guessing odds.
- Make an educated guess immediately: Don't leave blanks—guess based on partial knowledge or elimination.
- Use consistent notation: Develop symbols for "definitely return," "maybe return," and "random guess."
Strategic return hierarchy: When returning to flagged questions, follow this priority system:
- First return pass (5-7 minutes remaining): Attack problems that seem solvable with fresh perspective.
- Second return pass (2-3 minutes remaining): Focus on questions where partial credit through elimination is possible.
- Final 30 seconds: Ensure no blanks remain—random guess if necessary.
This approach requires overcoming students' perfectionist tendencies and teaching them that strategic abandonment is a sign of mathematical maturity, not failure.
Strategy 2: Implement checkpoint-based pacing control
Rather than hoping students will naturally maintain appropriate pace, establish specific checkpoints that provide early warning when timing goes off track. This system allows for proactive adjustments before situations become critical.
Paper ACT checkpoint system
- Question 15 by 15 minutes: Early pace verification—should feel comfortable and confident.
- Question 30 by 30 minutes: Critical midpoint assessment—if behind, begin aggressive skipping.
- Question 45 by 45 minutes: Final sprint begins—focus on completion over perfection.
- All questions attempted by 55 minutes: Reserve 5 minutes for returns and final guessing.
Digital ACT checkpoint system
- Question 11 by 12 minutes: Early rhythm check.
- Question 22 by 25 minutes: Midpoint evaluation—adjust strategy if needed.
- Question 34 by 38 minutes: Approaching peak difficulty—maintain focus on completion.
- All questions attempted by 45 minutes: Use remaining time for strategic returns.
Checkpoint recovery strategies
When students fall behind checkpoints, teach these escalating responses:
- 1-2 questions behind: Slightly increase pace while maintaining accuracy.
- 3-4 questions behind: Begin skipping problems that require more than 90 seconds.
- 5+ questions behind: Switch to rapid elimination and educated guessing mode.
Regular checkpoint practice builds internal timing awareness and prevents the panic that occurs when students suddenly realize they're far behind schedule.
Strategy 3: Develop question-type time allocation skills
Not all ACT Math questions deserve equal time investment. Students must quickly categorize problems and allocate appropriate time based on complexity and point value.
Time value recognition training
Teach students to rapidly assess and categorize problems:
- 30-45 second problems: Basic arithmetic, simple linear equations, formula substitution, percentage calculations
- 60-75 second problems: Multi-step algebra, standard geometry applications, coordinate geometry basics
- 90-120 second problems: Complex word problems, trigonometry applications, system of equations
- 2+ minute problems: Multi-concept integration, advanced function analysis, proof-style reasoning
Visual complexity indicators
Students should learn to identify time-intensive problems immediately:
- Dense text blocks: Word problems requiring translation and setup time
- Multiple diagrams: Geometry problems requiring spatial reasoning and relationship analysis
- Unusual notation: Advanced concepts that may require additional thinking time
- Question position: Later questions (40+) typically require more sophisticated approaches
Strategic time banking
Strong students should aim to complete early questions in 45-50 seconds, "banking" extra time for challenging problems later. This requires:
- Pattern recognition: Instant identification of familiar problem types
- Formula automation: Immediate recall without conscious effort or hesitation
- Mental math fluency: Quick calculation techniques for common operations
- Estimation skills: Recognition when approximate answers are sufficient
This differentiated approach ensures students invest their limited time where it will yield the highest point returns.
Strategy 4: Perfect answer sheet and navigation efficiency
Time lost to mechanical processes like bubbling answers or navigating between questions can accumulate to several minutes over a full section. Developing efficient habits in these areas provides more time for actual problem-solving.
Strategic bubbling for paper tests
Rather than bubbling after each question (which costs 8-10 seconds per question), teach batching strategies:
- 5-question batches: Answer 5 consecutive questions, then bubble all responses together.
- Page-based bubbling: Complete all questions on a test booklet page, then transfer answers.
- Time-remaining bubbling: When 10 minutes remain, prioritize completing all bubbling.
- Verification protocol: Always check that question numbers align perfectly with answer sheet positions.
Digital navigation mastery
For the enhanced digital ACT, students must develop fluency with:
- One-click flagging: Instant marking of questions for return without disrupting rhythm
- Keyboard shortcuts: Efficient movement between questions using arrow keys or number navigation
- Answer modification: Quick techniques for changing responses without time loss
- Progress tracking: Using built-in indicators to monitor pacing without losing focus
Answer choice elimination techniques
Systematic elimination saves time and improves guessing accuracy:
- Physical marking: On paper, visibly cross out eliminated choices with clear strokes
- Digital tools: Use available highlighting or striking features to mark eliminated options
- Logical ordering: Always eliminate most obviously incorrect answers first
- Confidence notation: Mark final answers with confidence levels (certain/likely/guess) for return prioritization
These mechanical efficiencies compound throughout the test, potentially providing 3-5 additional minutes for problem-solving.
Strategy 5: Build pressure tolerance through progressive training
Time management skills developed under comfortable practice conditions often collapse under actual test pressure. Students need systematic exposure to increasingly challenging timing scenarios to build real performance capabilities.
Progressive pressure protocol
Structure practice with escalating time pressure:
- Week 1: Individual topic practice with 75-second time limits (below test pressure)
- Week 2: Mixed practice sections with 60-second average (at test pressure)
- Week 3: Full sections with 50-second average targets (above test pressure)
- Week 4: Full practice tests with environmental distractions (extreme pressure simulation)
Micro-session timing drills
Build timing reflexes through focused exercises:
- 5-question sprints: Complete 5 varied problems in exactly 4 minutes, 30 seconds.
- Accuracy-speed balance tracking: Record both correct answers and completion times.
- Stress inoculation training: Practice with background noise, time pressure announcements, and interruptions.
- Recovery simulation: Practice regaining composure and timing after making mistakes.
Psychological pressure management
Teach students to handle timing stress through:
- Breathing reset techniques: 3-second deep breath protocols to regain composure when timing pressure builds
- Positive self-talk scripts: "I can catch up" and "strategic guessing is smart" rather than "I'm failing"
- Focus redirection skills: Concentration on current problem rather than time deficit anxiety
- Strategic acceptance mindset: Recognition that sometimes educated guessing is the mathematically optimal choice
Full simulation requirements
Students should complete multiple full-length math sections under exact test conditions, including identical timing, answer sheets, environmental conditions, and time-of-day scheduling. This builds familiarity with sustained pressure and prevents test-day surprises.
Through systematic application of these five strategies, students develop time management as a competitive advantage rather than a source of anxiety, allowing their mathematical knowledge to translate directly into ACT score improvements.
12 ACT Math Tips to Get High Marks
Here are 12 expert ACT Math tips tutors can use in sessions—and students can apply during prep and on test day—to cover everything from content mastery to pacing and confidence.
Tip 1: Understand the ACT Math format thoroughly
Section structure
The ACT Math section consists of 60 multiple-choice questions in 60 minutes for the traditional format, or 45 questions in 50 minutes for the enhanced digital version. The content spans pre-algebra, elementary and intermediate algebra, coordinate geometry, plane geometry, and trigonometry, but notably excludes calculus.
This comprehensive scope means students encounter everything from basic arithmetic to advanced trigonometric applications within a single section.
No formula sheet provided
There is no overall formula sheet provided for the ACT. Some individual questions may provide a formula, but the majority won't. This represents a fundamental difference from the SAT and creates a significant preparation challenge.
Students must memorize essential formulas including the quadratic formula, area and volume calculations, distance and midpoint formulas, and basic trigonometric ratios before test day. The absence of reference materials means that formula recall must become automatic to avoid wasting precious time during the exam.
Scoring rules and strategy
Each correct answer earns exactly one point, regardless of question difficulty. Crucially, there is no penalty for guessing, meaning incorrect or blank responses don't subtract points from the total score. This scoring structure creates a clear strategic imperative: students should attempt every question, even if they must guess randomly.
The equal point value of all questions also means that spending excessive time on one difficult problem while leaving easier questions unanswered represents poor strategy.
Reducing test-day anxiety
Thorough familiarity with the test format prevents surprises that can derail performance and allows students to focus entirely on problem-solving rather than navigating unfamiliar procedures.
As a tutor, you should simulate the real testing interface during practice sessions, including on-screen calculator usage, question flagging systems, and digital navigation tools.
Students who practice under authentic conditions develop automatic responses to format-specific challenges, freeing mental resources for mathematical reasoning on test day.
Tip 2: Prioritize High-Weight Topics
Identify the big areas
Not all ACT Math topics carry equal weight, and strategic preparation requires understanding this distribution. Approximately half of the problems cover Algebra and approximately 40% cover geometry. The remaining 10% covers concepts from middle school and some problems over high school Pre-calculus.
Specifically, algebra topics (including pre-algebra, elementary, and intermediate algebra) comprise roughly 66% of all questions, making them the clear priority for preparation time.
Geometry (both planar and coordinate) accounts for the significant majority of remaining questions, while trigonometry typically appears in only about four questions per test.
Run a diagnostic assessment
Before diving into content review, have students complete a full Math section under authentic timed conditions to establish baseline performance. Analyze their results not just for overall accuracy, but for domain-specific patterns—do they consistently miss geometry problems while excelling in algebra, or vice versa?
This diagnostic data becomes the foundation for creating a personalized study plan that addresses actual weaknesses rather than perceived ones. Document specific error types within each domain, such as whether geometry mistakes stem from formula confusion, spatial reasoning difficulties, or calculation errors.
Front-load study on core content
Given the weight distribution, algebra fundamentals should receive primary attention in early tutoring sessions. Focus on solving linear and quadratic equations, factoring techniques, working with ratios and proportions, and manipulating algebraic expressions. For geometry, emphasize angle properties, triangle theorems (including special right triangles), and circle formulas.
Students must memorize and practice applying key formulas repeatedly until recall becomes automatic—the quadratic formula, area and perimeter calculations, slope formula, and distance formula appear frequently enough to justify intensive memorization efforts.
Allocate tutoring time by impact
Structure your tutoring schedule to reflect question frequency and individual student error patterns. If a student struggles with coordinate geometry (9 questions) but excels in trigonometry (4 questions), allocate proportionally more time to coordinate geometry review.
Spend extra sessions on topics that combine high question frequency with high error rates for maximum score improvement potential. Reserve lighter review sessions for low-frequency areas like advanced trigonometric identities or complex number operations, which rarely appear and offer limited return on time investment.
Maintain balanced coverage
While prioritizing high-impact areas, avoid completely neglecting any topic domain. Even low-frequency topics like trigonometry can provide crucial points for students aiming for top scores, and complete gaps in knowledge create unnecessary vulnerability.
The key is working smarter rather than harder—ensuring basic familiarity with every domain while investing concentrated effort where it moves the score needle most effectively. This balanced approach prevents students from being blindsided by unexpected question types while maximizing preparation efficiency across the full content spectrum.
Tip 3: Practice timed sections regularly
Real, timed practice represents the bridge between content knowledge and test performance under pressure. Students often excel in untimed practice sessions only to struggle when facing the actual time constraints of the ACT Math section. Regular timed drills offer four critical benefits that transform preparation from theoretical knowledge into practical test-taking ability.
Pacing mastery
Consistent timed practice builds an internal rhythm that helps students naturally gauge their progress throughout the section. Rather than constantly checking the clock and losing focus, students develop an intuitive sense of the one minute per question pace that characterizes successful ACT Math performance.
This internal timing mechanism allows for better self-regulation during the actual test, as students can sense when they're falling behind schedule and need to adjust their approach without the anxiety-inducing shock of discovering major time deficits late in the section.
Stamina and focus development
The ACT Math section demands sustained concentration and mathematical reasoning for a full hour (or 50 minutes on digital format). Students who practice only individual problems or short problem sets often experience mental fatigue and declining accuracy in the latter portion of the actual test.
Regular full-section practice builds the cognitive endurance necessary to maintain sharp focus and computational accuracy through all questions, preventing the score-damaging errors that commonly occur when mental energy flags toward the end of the section.
Pressure-proofed strategy implementation
Test-taking strategies that seem natural during relaxed practice often break down under time pressure and test anxiety. Timed practice sessions allow students to rehearse and refine their approach to answer elimination, educated guessing, and problem-solving shortcuts until these techniques become automatic responses rather than conscious decisions.
Students learn to trust their strategic training even when stress levels rise, ensuring that their preparation translates directly into test-day performance improvements.
Realistic performance benchmarking
Only timed practice with official-style questions provides accurate assessment of current ability and meaningful measurement of improvement over time. Untimed practice scores create false confidence, while timed practice reveals genuine strengths and weaknesses that require attention.
These realistic benchmarks allow tutors and students to track both speed and accuracy gains, adjust preparation strategies based on actual performance data, and set appropriate score goals grounded in demonstrated capability rather than wishful thinking.
Tip 4: Teach Students to Skip and Return Strategically
Top-performing students understand that ACT Math success depends not just on mathematical ability, but on intelligent question selection and time allocation.
Flag time sinks immediately
Students should develop a strict internal timer that triggers strategic abandonment when a question stalls their progress for approximately 30 seconds. This threshold prevents the common trap where students invest 3-4 minutes in a single difficult problem while leaving multiple easier questions unattempted.
The key is teaching students to recognize the difference between productive thinking time and unproductive struggle—if they haven't identified a clear solution path within 30 seconds, the question becomes a candidate for later return rather than continued immediate effort.
Value every question equally
Since every question is multiple choice, and there is no penalty for guessing, all problems carry identical point value regardless of difficulty level. Students must internalize this reality and resist the natural tendency to persist on challenging problems simply because they seem more significant.
Trading three easily solvable questions for one time-consuming difficult problem represents poor strategic thinking—the mathematics of scoring demands that students prioritize accessibility over complexity when time becomes a limiting factor.
Guess before leaving
The absence of guessing penalties means students should never leave questions blank, even temporarily. Before moving on from a flagged question, students should make their best educated guess based on whatever partial understanding they've developed.
This approach ensures that even if time runs out before they can return, they haven't forfeited potential points. The guess also serves as a starting point if they do return later, as it represents their initial instincts about the problem before time pressure intensified.
Practice the routine systematically
Skip-and-return strategies only become effective through deliberate practice under timed conditions. Every practice session should include opportunities to flag questions, make strategic decisions about time allocation, and experience the process of returning to skipped problems with limited time remaining.
Students need to build comfort with the psychological challenge of leaving questions incomplete and develop confidence that this approach improves rather than harms their overall performance.
Use smart elimination on return
When returning to flagged questions, students should approach them with fresh perspective and refined strategy. Begin by physically crossing out obviously incorrect answer choices to improve guessing odds, then rely on estimation, logical reasoning, and partial knowledge to narrow remaining options.
Often, a brief break from a difficult problem allows students to see solution paths that weren't apparent during their initial encounter, making return visits surprisingly productive even under time pressure.
Tip 5: Focus on Reducing Careless Errors
Careless errors represent one of the most frustrating sources of point loss on the ACT Math section, as they typically occur on problems students understand conceptually but execute incorrectly due to rushed work or lack of systematic checking. Teaching students a quick, five-step accuracy checklist helps catch these costly mistakes before they become permanent score damage.
Stem review
Students should develop the habit of physically underlining or highlighting the specific question being asked, particularly the final phrase that indicates what value to find.
This simple step prevents the common error of solving for the wrong variable or quantity—for example, finding the radius when the question asks for diameter, or calculating the slope when the problem requests the y-intercept.
Taking two seconds to mark the target prevents minutes of accurate work that leads to an incorrect answer simply because the student solved for the wrong thing.
Sign and unit scan
Before beginning calculations, students should scan the problem for potential trouble spots including negative signs, unit specifications, and decimal placements.
Many errors stem from overlooking a negative sign in an equation, forgetting to convert between units (feet to inches, degrees to radians), or misplacing decimal points in calculations.
This brief scanning step helps students set up problems correctly from the start rather than discovering mistakes after completing lengthy calculations.
Scratch-pad clarity
Encourage students to rewrite complex problems neatly in their scratch space, numbering each step of their solution process.
Clear, organized work serves multiple purposes: it reduces computational errors that occur when work becomes messy and hard to follow, it makes checking work more efficient, and it helps students identify exactly where mistakes occurred if they need to revisit a problem.
The few seconds spent organizing work pays dividends in accuracy and error prevention.
Answer validation
Before bubbling their final answer, students should ask themselves whether their result makes sense in the context of the problem.
Does the calculated area seem reasonable for the given dimensions?
Is the percentage result between 0 and 100 where appropriate?
Does the answer actually address what the question asked for?
This sanity check catches many errors that occur when students correctly follow mathematical procedures but apply them to the wrong scenario or misinterpret the problem setup.
Strategic error catching
In the last 10 seconds of work on any problem, students should perform a quick visual scan of their calculation work, paying special attention to flagged items or complex multi-step problems where errors commonly occur.
This isn't a complete re-solution but rather a rapid check for obvious mistakes like sign errors, miscopied numbers, or calculation slips.
While time pressure makes extensive checking impossible, this brief final review catches many errors with minimal time investment and can be the difference between a good score and a great one.
Tip 6: Reinforce concepts with spaced repetition
Formula mastery represents a critical foundation for ACT Math success, yet traditional cramming approaches often fail to create lasting retention. Since there is no overall formula sheet provided for the ACT, students must develop automatic recall of essential formulas through systematic reinforcement rather than hoping that occasional review will suffice.
Digital flashcards with algorithmic scheduling
Build comprehensive digital flashcard decks using platforms like Anki or Quizlet that incorporate spaced repetition algorithms designed to optimize long-term retention.
Focus on must-know formulas including the quadratic formula, circle area and circumference calculations, right triangle ratios (SOH-CAH-TOA), distance and midpoint formulas, and basic geometric area/volume calculations.
These platforms automatically adjust review frequency based on recall performance—formulas students struggle with appear more frequently, while well-mastered formulas require less frequent reinforcement.
Daily review sessions of just 5-10 minutes using these algorithmic schedules prove far more effective than sporadic intensive cramming sessions.
Session kick-off mini-quizzes
Begin each tutoring session with a focused 3-question mini-quiz covering 2-3 core formulas from recent study topics. This brief assessment serves multiple purposes: it activates prior knowledge before new learning, identifies formulas that need additional reinforcement, and creates accountability for ongoing formula practice between sessions.
The key is immediate application—after students recall each formula, have them solve a related practice problem that requires using that formula in context. This approach bridges the gap between rote memorization and practical application, ensuring that formula knowledge translates into problem-solving capability.
Distributed practice benefits
Spaced repetition leverages the psychological spacing effect, where information reviewed at increasing intervals becomes more deeply embedded in long-term memory than information studied intensively in short periods.
For ACT Math preparation, this means that 10 minutes of daily formula practice over several weeks produces dramatically better retention than cramming formulas for hours immediately before the test.
Students who implement consistent spaced repetition report that formulas become automatic rather than effortful to recall, freeing cognitive resources for complex problem-solving during the actual test.
Integration with problem-solving practice
Rather than treating formula memorization as separate from problem practice, integrate both approaches by having students identify and state relevant formulas before attempting practice problems.
When students encounter a geometry problem, they should first articulate the relevant area or volume formula before beginning calculations. This integration reinforces the connection between formula knowledge and practical application while building the rapid formula recognition skills essential for success under time pressure.
The combination of spaced repetition for raw memorization and contextual application ensures that formula knowledge becomes both durable and accessible when needed most.
Tip 7: Use data to track weak areas
Effective ACT Math preparation requires moving beyond general practice to precision-targeted improvement based on objective performance data.
Run regular diagnostic assessments
Schedule full Math section practice tests under authentic timed conditions every 2-3 weeks throughout the preparation period to establish reliable performance baselines and track improvement trajectories.
Break down results by major topic areas including algebra, geometry, and trigonometry, then drill deeper into subtopic performance such as linear equations, quadratic functions, circle properties, and coordinate geometry.
This granular analysis reveals whether struggles stem from broad conceptual gaps (struggling with all algebra) or specific skill deficits (difficulty only with systems of equations), allowing for precisely targeted intervention strategies.
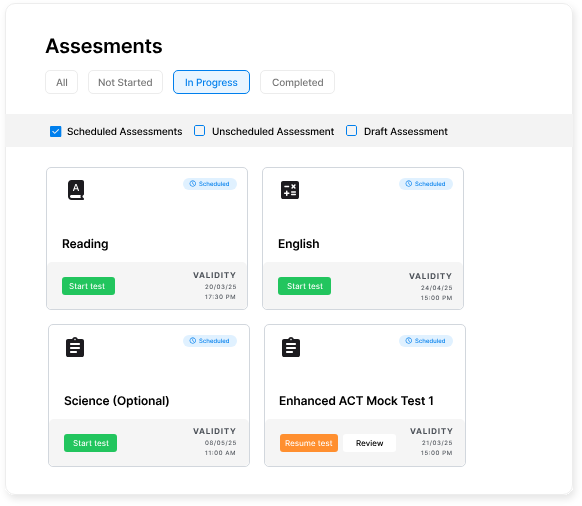
Track progress over time with multiple metrics
Chart both composite Math scores and section-specific performance to identify improvement patterns, plateaus, or unexpected declines that might indicate fatigue or strategy problems.
Additionally, monitor time per question across different practice sessions to identify pacing issues—students might improve accuracy while developing problematic time management, or conversely, speed up their work while sacrificing precision.
Comprehensive tracking reveals whether improvements in one area come at the expense of others, enabling balanced optimization of overall performance.
Identify and classify error patterns
Systematically categorize every mistake as conceptual (didn't know the mathematical content), careless (computational slips, misreading, or transcription errors), or pacing-related (rushed work due to time pressure).
This classification system reveals whether student struggles stem from knowledge gaps that require content review, attention issues that need accuracy protocols, or time management problems that demand strategy adjustment.
If many errors cluster in the careless category, reinforce careful reading and checking routines; if they concentrate on specific topics, schedule intensive targeted drills for those content areas.
Leverage technology for automated analysis
Utilize comprehensive analytics platforms like EdisonOS or similar dashboard systems that automatically log incorrect responses, categorize them by topic and difficulty level, and highlight timing patterns that drain efficiency.
These systems remove the manual burden of data collection while providing sophisticated analysis that might be missed through informal observation. The automated categorization and progress tracking capabilities allow tutors to spend time on instruction rather than data management while ensuring that no performance patterns go unnoticed.

Create action plans from data insights
Transform data analysis into concrete instructional decisions by establishing clear thresholds for intervention—for example, if a student misses more than 40% of coordinate geometry questions across multiple practice sessions, schedule dedicated coordinate geometry review.
Similarly, if timing data shows students spending more than 90 seconds on average for trigonometry questions, implement specific time management strategies for that topic area. Data-driven preparation ensures that every tutoring minute addresses actual rather than assumed weaknesses, maximizing score improvement efficiency.
Tip 8: Simulate test-day mindset and conditions
Preparing students for the ACT Math section extends far beyond mathematical content mastery—it requires developing the ability to perform under the unique pressures, fatigue, and logistical challenges of actual test day.
Students who excel in comfortable practice environments often struggle when faced with the psychological and physical demands of the real testing experience, making simulation-based preparation essential for translating knowledge into performance.
Full-length practice tests under authentic conditions
Schedule complete four-section practice exams at the same morning hour when students will take their actual ACT, using proper timing sequences with official breaks to build the sustained concentration and mental stamina required for peak performance.
The Math section doesn't exist in isolation—students must maintain mathematical precision even after completing potentially challenging English, Reading, and Science sections that may have created fatigue or anxiety.
Debrief how performance in earlier sections affects mathematical confidence and focus, teaching students to compartmentalize difficulties and approach each section with renewed energy rather than carrying forward frustration or self-doubt.
Realistic testing environment simulation
Practice using authentic materials and conditions that mirror the actual test experience as closely as possible. For paper tests, students should practice exclusively with bubble sheets and the specific calculator they plan to use on test day, while digital test preparation should occur on the official ACT interface to build familiarity with navigation, flagging, and tool usage.
Simulate environmental details including wearing masks if required, sitting at a standard desk for extended periods, and managing the physical discomfort that can distract from mathematical reasoning.
Consider arranging proctored mock exams that introduce the formality and psychological pressure of actual exam rooms, helping students acclimate to external oversight and time announcements.
Mental focus and anxiety management techniques
Teach practical stress management strategies that students can deploy during the actual test without drawing attention or consuming significant time. Simple breathing exercises—such as taking three deep breaths before beginning the Math section—can reset focus and reduce physiological anxiety responses.
Develop positive self-talk scripts that students can use when encountering difficult problems, such as "I'll skip and come back to this" or "I've prepared well and can handle this challenge."
Encourage brief mindfulness resets between sections or when transitioning from difficult to easier problems, helping students maintain emotional equilibrium throughout the testing experience.
Game-day logistics and preparation
Address practical considerations that can create unnecessary stress and distraction on test morning. Ensure students understand the importance of adequate sleep (7-8 hours) and appropriate nutrition—a light breakfast with sustained energy sources rather than heavy or unfamiliar foods that might cause discomfort.
Create comprehensive packing checklists including admission tickets, acceptable identification, approved calculators, and adequate pencils, while also reviewing prohibited items to avoid test-day complications.
Handling these logistics well in advance allows students to focus entirely on performance rather than worrying about procedural details during the critical testing period.
Confidence building through evidence-based reinforcement
Systematically highlight concrete evidence of student improvement throughout the preparation process, transforming abstract progress into specific confidence anchors. Reference mastered concepts explicitly—"You've consistently solved inequality questions correctly in recent practice sessions—you're ready for those on test day."
Help students reframe pre-test anxiety as normal and manageable rather than threatening, emphasizing that thorough preparation provides the foundation for success regardless of specific questions encountered.
This evidence-based confidence building creates genuine self-assurance grounded in demonstrated capability rather than hollow encouragement, enabling students to approach the test with calm focus rather than paralyzing anxiety.
Tip 9: Demystify word problems and multi-step questions
Word problems represent one of the most significant anxiety sources for ACT Math students, not because they lack mathematical knowledge, but because they struggle to extract mathematical relationships from dense verbal descriptions.
Read actively and translate mathematical language
Students should approach word problems as translation exercises rather than pure mathematical challenges, beginning by underlining or highlighting key numerical data, variable relationships, and the specific question being asked.
After this initial scan, require students to restate the problem in their own words, stripping away extraneous narrative details to reveal the core mathematical relationships. This translation process helps students differentiate between relevant information that drives the solution and decorative context that can distract from the essential mathematical task.
The act of restating also forces students to confirm their understanding before beginning calculations, preventing the common error of solving the wrong problem accurately.
Break complex problems into sequential steps
Multi-step word problems become manageable when students learn to decompose them into numbered, sequential tasks that build toward the final answer.
For example, a problem might require students to (1) find the area of a rectangle, (2) use that area to determine material costs, and (3) calculate total expenses including tax.
By explicitly numbering each step and solving one component at a time, students avoid the overwhelming feeling of facing an impossibly complex problem while also preventing cascading errors where mistakes in early calculations corrupt all subsequent work.
This methodical approach also makes checking work more straightforward, as students can verify each step independently.
Make abstract relationships visual
Encourage students to create simple sketches, diagrams, or organizational tables that transform verbal descriptions into visual representations of mathematical relationships.
Geometry word problems benefit from labeled shapes that show given measurements and unknown values, while rate problems become clearer when students draw timelines or distance diagrams. Even algebraic word problems often benefit from simple charts that organize given information and unknown variables.
These visual aids serve as external memory supports that reduce cognitive load while also helping students identify relationships that might not be apparent from text alone.
Identify the core mathematical concept
Behind every word problem lies a fundamental mathematical skill or concept that the problem is designed to assess. Train students to ask themselves, "What specific mathematical knowledge is this problem testing?" before beginning calculations.
Is this fundamentally a proportion problem disguised as a recipe scenario?
Does this distance/rate/time story problem require the basic formula d = rt?
Is this percentage problem hiding behind a sales tax context?
Identifying the underlying mathematical structure helps students select appropriate formulas and solution strategies while building confidence through recognition of familiar patterns.
Practice with reflection and pattern recognition
Use official ACT word problems during practice sessions, but extend beyond simple solution verification to include structured reflection on problem-solving approaches.
After solving each problem, discuss any misleading details, unnecessary information, or potential traps that might confuse students during actual testing. Help students recognize common word problem categories and the mathematical approaches they typically require.
With repeated practice and reflection, students develop pattern recognition skills that allow them to quickly categorize new word problems and apply appropriate solution strategies, transforming their attitude from "I hate word problems" to "Let me systematically break this down into manageable pieces."
Tip 10: Build mental math and smart calculator skills
Effective ACT Math performance requires balancing mental calculation fluency with strategic calculator usage. Students who rely too heavily on calculators for simple operations waste precious time, while those who attempt complex calculations mentally often make computational errors that cost points despite correct mathematical reasoning.
Practice mental math drills for speed and automaticity
Begin each tutoring session with quick arithmetic warm-ups including basic multiplication facts (15 × 12, 7 × 8), simple division (75 ÷ 5, 84 ÷ 7), and estimation skills (√50 ≈ 7, 15% of 80 ≈ 12). The goal is developing instant recall of fundamental calculations so that trivial arithmetic doesn't consume cognitive resources during problem-solving.
Students should achieve automatic recognition of common fraction-decimal-percentage equivalents (0.75 = 75% = 3/4) and basic square roots up to 144. This foundational fluency allows students to focus mental energy on mathematical reasoning rather than computational mechanics during the actual test.
Teach strategic estimation techniques
Estimation serves two critical purposes on the ACT Math section—eliminating implausible answer choices quickly and providing sanity checks for complex calculations. When exact calculations become unwieldy, students should round values to convenient numbers and determine which answer choice falls "in the ballpark" of their estimate.
For example, if a problem requires calculating 47 × 23, students can estimate using 50 × 20 = 1000 to quickly eliminate answer choices that are far from this range. Estimation also catches major errors—if careful calculation returns 512 for a problem that clearly should yield an answer near 50, students know to re-evaluate their approach rather than trusting an obviously incorrect result.
Know your calculator and use it strategically
Students should achieve complete fluency with their chosen calculator's essential functions including parentheses usage, square root calculations, trigonometric functions, and answer recall features before test day. However, calculator usage should be reserved for genuinely complex arithmetic such as long division, multi-step decimal calculations, or trigonometric evaluations.
Simple operations like 8 + 15 or 6 × 7 should be performed mentally to save time and maintain problem-solving momentum. The decision between mental calculation and calculator usage should become automatic based on the complexity and error-risk of each computation.
Master advanced calculator techniques for efficiency
Intermediate calculator skills can significantly improve efficiency during complex multi-step problems. Students should learn to store intermediate results in memory or use the ANS (answer) key to avoid retyping long decimal values that introduce transcription errors. Many calculators offer quick toggling between fraction and decimal modes, allowing students to verify their work or choose the most convenient form for subsequent calculations.
These techniques prove especially valuable during coordinate geometry problems or statistical calculations where intermediate values feed into multiple subsequent computations.
Develop balanced calculation judgment
The most effective students develop intuitive judgment about when mental math offers speed advantages versus when calculator precision becomes essential. Simple addition, basic multiplication facts, and obvious percentage calculations should be performed mentally to maintain rhythm and save time. Complex operations involving multiple decimal places, trigonometric functions, or multi-step algebraic manipulations benefit from calculator support to ensure accuracy.
Students need practice making these judgment calls quickly and confidently, as hesitation about calculation methods can waste as much time as poor computational choices. This balanced approach maximizes both speed and accuracy while building confidence in calculation decisions under time pressure.
Tip 11: Review mistakes and adjust strategies after each practice
Systematic mistake analysis transforms errors from simple point losses into powerful learning opportunities that drive targeted improvement. Rather than viewing mistakes as failures, effective tutoring treats them as diagnostic data that reveals exactly where students need additional support and strategy refinement.
Categorize mistakes for targeted intervention
After each practice session, systematically classify every error into specific categories that suggest different remediation approaches. Conceptual errors indicate that students didn't fully grasp the underlying mathematical principle being tested, requiring content review and additional instruction.
Careless slips involve computational mistakes, copying errors, or transcription problems where students understood the concept but failed in execution. Timing issues result from rushed work or running out of time, suggesting the need for pacing strategy adjustment.
Misread questions stem from misunderstanding what was actually being asked, pointing to the need for active reading techniques and question analysis skills. This categorization system ensures that tutoring time addresses the actual source of errors rather than applying generic remediation.
Investigate root causes thoroughly
Move beyond surface-level error identification to explore why each mistake occurred at a deeper level. Discuss whether conceptual errors stem from vocabulary gaps, formula confusion, or incomplete understanding of mathematical relationships. Examine whether careless mistakes result from working too quickly, inadequate scratch paper organization, or insufficient checking routines.
Determine if timing issues reflect poor question prioritization, excessive time on difficult problems, or inadequate practice with timed conditions. This diagnostic conversation reveals the specific intervention strategies most likely to prevent similar errors in future practice sessions and on the actual test.
Implement active correction and reinforcement
Require students to re-solve each missed question correctly using proper mathematical reasoning and clear written work. This active correction process ensures that students don't simply learn the right answer but understand the complete solution pathway that leads to correct responses.
Follow up by assigning 2-3 similar problems focusing on the same mathematical concept during subsequent tutoring sessions, providing distributed practice that reinforces learning and builds confidence. This approach transforms isolated mistakes into comprehensive learning experiences that strengthen understanding across related problem types.
Maintain comprehensive error logs for pattern recognition
Create detailed records including question numbers, mistake categories, correct solutions, and key takeaway lessons for each error across all practice sessions. These logs become invaluable diagnostic tools that reveal patterns invisible during individual practice sessions—for example, consistent struggles with coordinate geometry or recurring careless errors during time pressure.
Review error logs before each new practice session to refresh student awareness of past pitfalls and reinforce lessons learned from previous mistakes. This systematic approach prevents students from repeating the same errors while building metacognitive awareness of their individual challenge areas.
Adjust preparation strategies based on error patterns
Use error analysis to drive strategic modifications in preparation approach and tutoring focus. If mistakes consistently stem from time pressure and rushing, dedicate additional practice time to pacing techniques, skip-and-return strategies, and timed condition simulation.
When errors cluster around specific mathematical topics, allocate extra review sessions to those content areas and implement specialized drill exercises targeting identified weaknesses. If careless mistakes dominate, emphasize accuracy protocols, checking routines, and scratch paper organization techniques.
This data-driven approach ensures that preparation time addresses actual performance limitations rather than perceived weaknesses, maximizing the effectiveness of limited tutoring hours.
Tip 11: Review mistakes and adjust strategies after each practice
Systematic mistake analysis transforms errors from simple point losses into powerful learning opportunities that drive targeted improvement. Rather than viewing mistakes as failures, effective tutoring treats them as diagnostic data that reveals exactly where students need additional support and strategy refinement.
Categorize mistakes for targeted intervention
After each practice session, systematically classify every error into specific categories that suggest different remediation approaches. Conceptual errors indicate that students didn't fully grasp the underlying mathematical principle being tested, requiring content review and additional instruction.
Careless slips involve computational mistakes, copying errors, or transcription problems where students understood the concept but failed in execution. Timing issues result from rushed work or running out of time, suggesting the need for pacing strategy adjustment.
Misread questions stem from misunderstanding what was actually being asked, pointing to the need for active reading techniques and question analysis skills. This categorization system ensures that tutoring time addresses the actual source of errors rather than applying generic remediation.
Investigate root causes thoroughly
Move beyond surface-level error identification to explore why each mistake occurred at a deeper level. Discuss whether conceptual errors stem from vocabulary gaps, formula confusion, or incomplete understanding of mathematical relationships. Examine whether careless mistakes result from working too quickly, inadequate scratch paper organization, or insufficient checking routines.
Determine if timing issues reflect poor question prioritization, excessive time on difficult problems, or inadequate practice with timed conditions. This diagnostic conversation reveals the specific intervention strategies most likely to prevent similar errors in future practice sessions and on the actual test.
Implement active correction and reinforcement
Require students to re-solve each missed question correctly using proper mathematical reasoning and clear written work. This active correction process ensures that students don't simply learn the right answer but understand the complete solution pathway that leads to correct responses.
Follow up by assigning 2-3 similar problems focusing on the same mathematical concept during subsequent tutoring sessions, providing distributed practice that reinforces learning and builds confidence. This approach transforms isolated mistakes into comprehensive learning experiences that strengthen understanding across related problem types.
Maintain comprehensive error logs for pattern recognition
Create detailed records including question numbers, mistake categories, correct solutions, and key takeaway lessons for each error across all practice sessions. These logs become invaluable diagnostic tools that reveal patterns invisible during individual practice sessions—for example, consistent struggles with coordinate geometry or recurring careless errors during time pressure.
Review error logs before each new practice session to refresh student awareness of past pitfalls and reinforce lessons learned from previous mistakes. This systematic approach prevents students from repeating the same errors while building metacognitive awareness of their individual challenge areas.
Adjust preparation strategies based on error patterns
Use error analysis to drive strategic modifications in preparation approach and tutoring focus. If mistakes consistently stem from time pressure and rushing, dedicate additional practice time to pacing techniques, skip-and-return strategies, and timed condition simulation.
When errors cluster around specific mathematical topics, allocate extra review sessions to those content areas and implement specialized drill exercises targeting identified weaknesses. If careless mistakes dominate, emphasize accuracy protocols, checking routines, and scratch paper organization techniques.
This data-driven approach ensures that preparation time addresses actual performance limitations rather than perceived weaknesses, maximizing the effectiveness of limited tutoring hours.
Helping students succeed with proven ACT math tips and strategies
Teaching ACT Math extends far beyond drilling students through endless practice problems—it requires implementing comprehensive strategies that build both mathematical competence and test-taking confidence.
The difference between students who struggle with ACT Math and those who excel lies not just in mathematical knowledge, but in their ability to execute that knowledge efficiently under extreme time pressure while managing test anxiety and strategic decision-making.
Effective ACT Math tutoring combines multiple strategic approaches working in harmony. By prioritizing high-weight topics like algebra and geometry that comprise the majority of test questions, tutors ensure that limited preparation time yields maximum score improvement potential. Fine-tuning pacing strategies through systematic practice with skip-and-return techniques prevents students from sacrificing easy points while struggling with time-consuming difficult problems.
Success in ACT Math tutoring ultimately depends on helping students develop both the skills and mindset necessary for peak performance under pressure. When students master these strategic approaches through deliberate practice and reflection, they experience the confidence that comes from knowing they're prepared for whatever the test presents.
The result is not just higher scores, but students who approach mathematical challenges with systematic thinking and strategic awareness that serves them well beyond the ACT.
Book a free demo to discover how EdisonOS can streamline your ACT Math prep and drive better results.
Frequently asked questions
Tutors Edge by EdisonOS
in our newsletter, curated to help tutors stay ahead!
Tutors Edge by EdisonOS
Get Exclusive test insights and updates in our newsletter, curated to help tutors stay ahead!
Recommended Reads
Recommended Podcasts






.png)




.png)
.webp)
